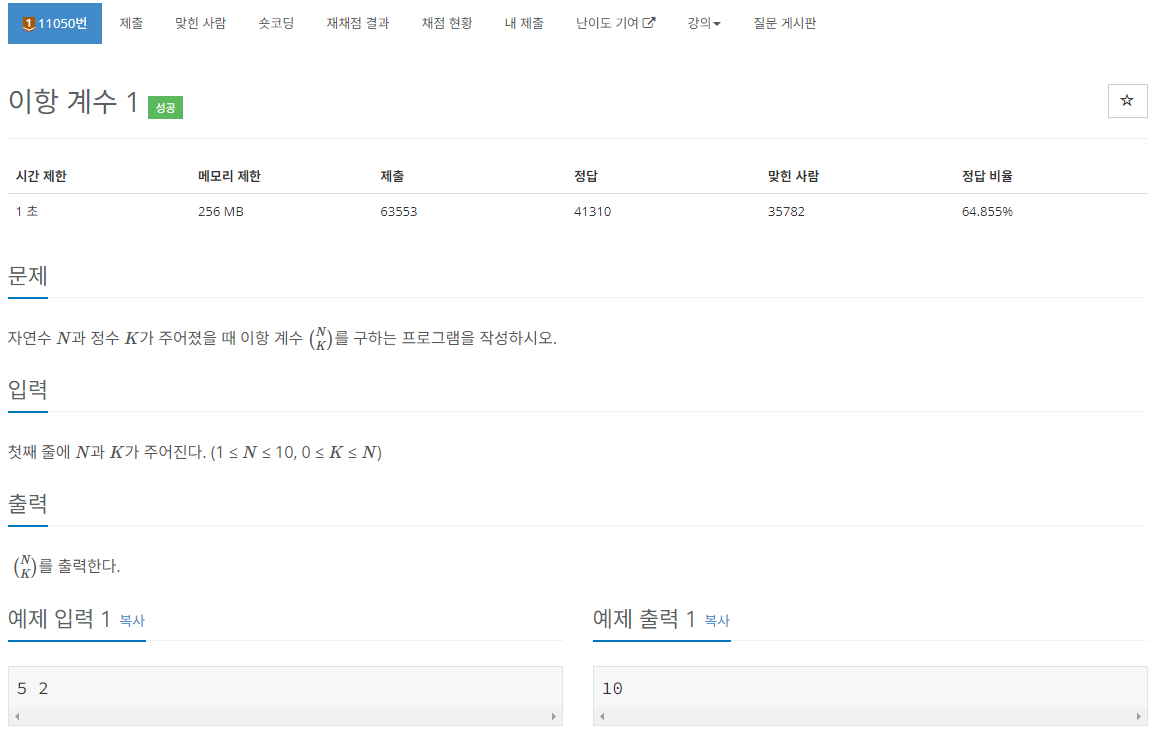
해당 문제에 대해 3가지 방법으로 풀어보았다.
- 조합 공식 및 반복문 사용
- 조합 공식 및 재귀(팩토리얼) 사용
- dp 및 재귀 사용
처음 풀었을 때는 단순하게 조합 공식인 아래 공식을 사용하여 풀었다.
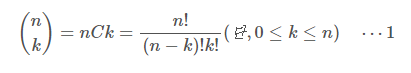
성공 소스 1 - 반복문
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int a = 1;
int b = 1;
int c = 1;
for (int i = 2; i <= n; i++) a *= i;
for (int i = 2; i <= n - k; i++) b *= i;
for (int i = 2; i <= k; i++) c *= i;
System.out.println(a / (b * c));
br.close();
}
두 번째 풀이는 공식의 팩토리얼이 있어 재귀를 사용하여 풀어봤다.
성공 소스 2 - 재귀
public class _11050_anotherSolving1 {
private static int factorial(int num) {
if (num == 0) return 1;
return num * factorial(num - 1);
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
// nCr = n! / (n - r)! * r!
System.out.println(factorial(n) / (factorial(n - k) * factorial(k)));
br.close();
}
}
이항 계수: 두 개의 항(이항)을 전개하여 계수로 나타낸 것.
$(a + b)^n$을 전개하였을 때의 계수.
이항계수에 대해 자세히 모르고 있어 찾아보던 중 고등학생 때 들어본 파스칼 삼각형과 연관이 있었다.
파스칼 삼각형
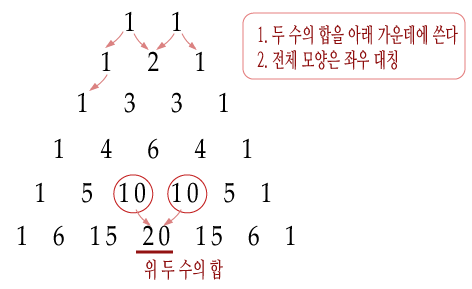
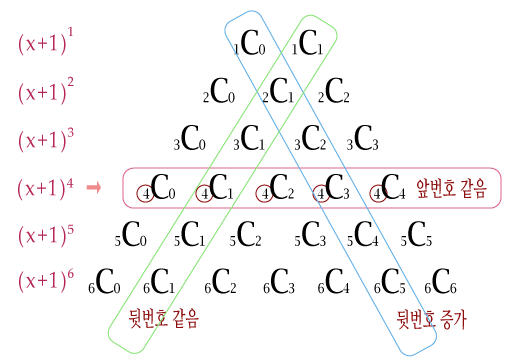
좌측의 이미지에서 위 두 수의 합이 가운데 아래 값인 것을 확인하면 공식을 아래와 같이 세울 수 있다.
nCr = n-1Cr-1 + n-1Cr
5C2 = 4C1 + 4C2
=> 10
아래 구현소스는 위 공식과 메모이제이션을 활용한 3번째 풀이 방법.
- 메모이제이션이란 동일한 계산을 반복할 때 이전에 계산한 값을 미리 저장해 놓는 기술로 동적 계획법의 핵심 기술.
성공 소스 - dp
public class _11050_anotherSolving2 {
private static Integer[][] dp;
private static int binomial(int n, int k) {
// 이미 연산된 적 있는 경우 기존 결과값 반환
if (dp[n][k] != null) {
return dp[n][k];
}
/*
n개 중에 k개를 뽑으니 n과 k가 같으면 1
k가 0이면 한 개도 뽑지 않으니 1
*/
if (n == k || k == 0) {
return dp[n][k] = 1;
}
return dp[n][k] = binomial(n - 1, k - 1) + binomial(n - 1, k);
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
dp = new Integer[n + 1][k + 1];
System.out.println(binomial(n, k));
br.close();
}
}
- 참고 블로그
https://blog.naver.com/vollollov/220947452823
파스칼의 삼각형과 이항계수의 성질
이번 포스트에서 살펴볼 내용은 파스칼의 삼각형을 이용한 이항계수의 성질입니다. 이름은 파스칼의 삼각형...
blog.naver.com
https://st-lab.tistory.com/159
[백준] 11050번 : 이항 계수 1 - JAVA [자바]
www.acmicpc.net/problem/11050 11050번: 이항 계수 1 첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 10, 0 ≤ \(K\) ≤ \(N\)) www.acmicpc.net 문제 알고리즘 [접근 방법] 이항 계수(Binomial coefficient) 문제 자체는 매
st-lab.tistory.com
'백준' 카테고리의 다른 글
| [백준] 11561번 : 징검다리 - JAVA (0) | 2024.03.31 |
|---|---|
| [백준] 1966번 : 프린터 큐- JAVA (0) | 2024.03.28 |
| [백준] 골드 달성 후기 (0) | 2024.03.24 |
| [백준] 1654번 : 랜선 자르기 - JAVA (0) | 2024.03.19 |
| [백준] 1920번 : 수 찾기 - JAVA (4) | 2024.03.17 |

해당 문제에 대해 3가지 방법으로 풀어보았다.
- 조합 공식 및 반복문 사용
- 조합 공식 및 재귀(팩토리얼) 사용
- dp 및 재귀 사용
처음 풀었을 때는 단순하게 조합 공식인 아래 공식을 사용하여 풀었다.
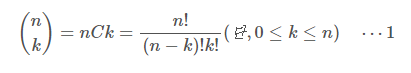
성공 소스 1 - 반복문
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int a = 1;
int b = 1;
int c = 1;
for (int i = 2; i <= n; i++) a *= i;
for (int i = 2; i <= n - k; i++) b *= i;
for (int i = 2; i <= k; i++) c *= i;
System.out.println(a / (b * c));
br.close();
}
두 번째 풀이는 공식의 팩토리얼이 있어 재귀를 사용하여 풀어봤다.
성공 소스 2 - 재귀
public class _11050_anotherSolving1 {
private static int factorial(int num) {
if (num == 0) return 1;
return num * factorial(num - 1);
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
// nCr = n! / (n - r)! * r!
System.out.println(factorial(n) / (factorial(n - k) * factorial(k)));
br.close();
}
}
이항 계수: 두 개의 항(이항)을 전개하여 계수로 나타낸 것.
이항계수에 대해 자세히 모르고 있어 찾아보던 중 고등학생 때 들어본 파스칼 삼각형과 연관이 있었다.
파스칼 삼각형


좌측의 이미지에서 위 두 수의 합이 가운데 아래 값인 것을 확인하면 공식을 아래와 같이 세울 수 있다.
nCr = n-1Cr-1 + n-1Cr
5C2 = 4C1 + 4C2
=> 10
아래 구현소스는 위 공식과 메모이제이션을 활용한 3번째 풀이 방법.
- 메모이제이션이란 동일한 계산을 반복할 때 이전에 계산한 값을 미리 저장해 놓는 기술로 동적 계획법의 핵심 기술.
성공 소스 - dp
public class _11050_anotherSolving2 {
private static Integer[][] dp;
private static int binomial(int n, int k) {
// 이미 연산된 적 있는 경우 기존 결과값 반환
if (dp[n][k] != null) {
return dp[n][k];
}
/*
n개 중에 k개를 뽑으니 n과 k가 같으면 1
k가 0이면 한 개도 뽑지 않으니 1
*/
if (n == k || k == 0) {
return dp[n][k] = 1;
}
return dp[n][k] = binomial(n - 1, k - 1) + binomial(n - 1, k);
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
dp = new Integer[n + 1][k + 1];
System.out.println(binomial(n, k));
br.close();
}
}
- 참고 블로그
https://blog.naver.com/vollollov/220947452823
파스칼의 삼각형과 이항계수의 성질
이번 포스트에서 살펴볼 내용은 파스칼의 삼각형을 이용한 이항계수의 성질입니다. 이름은 파스칼의 삼각형...
blog.naver.com
https://st-lab.tistory.com/159
[백준] 11050번 : 이항 계수 1 - JAVA [자바]
www.acmicpc.net/problem/11050 11050번: 이항 계수 1 첫째 줄에
st-lab.tistory.com
'백준' 카테고리의 다른 글
| [백준] 11561번 : 징검다리 - JAVA (0) | 2024.03.31 |
|---|---|
| [백준] 1966번 : 프린터 큐- JAVA (0) | 2024.03.28 |
| [백준] 골드 달성 후기 (0) | 2024.03.24 |
| [백준] 1654번 : 랜선 자르기 - JAVA (0) | 2024.03.19 |
| [백준] 1920번 : 수 찾기 - JAVA (4) | 2024.03.17 |
